Kaj kaže slika?
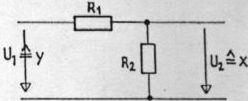
- praktičen primer proporcionalnega člena
- praktičen primer integralnega člena
- praktičen primer diferencialnega člena
- praktičen primer zakasnilnega člena
- praktičen primer PT1 člena
- praktičen primer DT1 člena ali realnega diferencialnega člena
- praktičen primer PT2 člena
Kaj kaže slika?
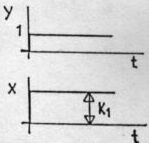
- prehodno funkcijo proporcionalnega člena
- prehodno funkcijo integralnega člena
- prehodno funkcijo diferencialnega člena
- prehodno funkcijo zakasnilnega člena
- prehodno funkcijo PT1 člena
- prehodno funkcijo DT1 člena ali realnega diferencialnega člena
- prehodno funkcijo PT2 člena
Kaj kaže slika?
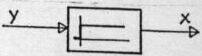
- simbol proporcionalnega člena
- simbol integralnega člena
- simbol diferencialnega člena
- simbol zakasnilnega člena
- simbol PT1 člena
- simbol DT1 člena ali realnega diferencialnega člena
- simbol PT2 člena
Kako še drugače imenujemo člen na sliki?

- delilnik napetosti
- elektromotor z reduktorjem
- tahogenerator
- transportni trak za dovajanje premoga
- diferenciator
- integrator
- vzporedni nihajni krog
Koliko elementov, ki so sposobni hraniti energijo, vsebuje vezje na sliki?
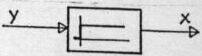

- 0
- 1
- 2
- 3
- 4
Katerega reda je torej člen, ki ga vidimo na sliki?
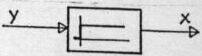

- člen ničelnega reda
- člen prvega reda
- člen drugega reda
- člena ni mogoče uvrstiti v nobeno od naštetih skupin
Kateri osnovni testni signal je uporabljen za določanje lastnosti člena na sliki?

- enotina stopnica
- enotin impulz
- enakomerno naraščajoča strmina z naklonom ene enote
Kako se člen na sliki odziva na vzbujanje z enotino stopnico? Kateri od opisov prehodne funkcije torej ustreza sliki?
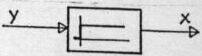


- odziv na enotino stopnico je enakomerno naraščanje izhodnega signala in sicer za eno enoto v času integracijske konstante Ti
- odziv na enotino stopnico je prav tako enotina stopnica, le da je pomnožena z ojačevalnim faktorjem K1
- odziv na enotino stopnico je prav tako enotina stopnica, le da je zakasnjena za mrtvi čas Tm
- odziv na enotino stopnico je neskončno kratek in neskončno velik impulz, ki se pojavi istočasno s prehodom stopnice iz nizkega stanja v visoko stanje
- odziv na enotino stopnico je naravna ali eksponetna krivulja s časovno konstanto "tau", ki je po obliki enaka časovnemu poteku napetosti kondenzatorja pri polnenju
- odziv na enotino stopnico je naravna ali eksponetna krivulja s časovno konstanto "tau", ki je po obliki enaka časovnemu poteku toka skozi kondenzator pri polnenju
- odziv na enotino stopnico je krivulja, ki je enaka krivulji dušenega nihanja nihajnega kroga, pri kateri sta značilna podatka največja amplituda prenihanja Apr in perioda nihanja Tl
Kateri člen ustreza spodnjemu opisu?
Ti členi so sestavi, pri katerih je sprememba izhodne veličine sorazmerna spremembi vhodne veličine. Pri teh členih ni časovne zakasnitve med vhodnim in izhodnim signalom. To pomeni, da so ti členi neskončno hitri. Lep primer je vezje, sestavljeno iz dveh ohmskih uporov.- proporcionalni člen
- integralni člen
- diferencialni člen
- zakasnilni člen
- PT1 člen
- DT1 člen ali realni diferencialni člen
- PT2 člen
Kateri opis ustreza sliki?
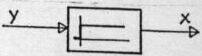


- Ti členi so sestavi, pri katerih je sprememba izhodne veličine sorazmerna spremembi vhodne veličine. Pri teh členih ni časovne zakasnitve med vhodnim in izhodnim signalom. To pomeni, da so ti členi neskončno hitri. Lep primer je vezje, sestavljeno iz dveh ohmskih uporov.
- Ti členi so členi, pri katerih je hitrost spremembe izhodne veličine sorazmerna velikosti vhodne veličine. Če je vrednost vhodne veličine velika, se izhodna veličina spreminja hitro, če pa je vhodna veličina majhna, se izhodna veličina spreminja počasi. Sorazmernostni faktor Ti imenujemo integracijska časovna konstanta, pove pa, v kolikšnem času se spremeni velikost izhodne veličine za eno enoto oziroma, v kolikšnem času doseže izhodni signal vrednost vhodnega signala. S pomočjo prehodne funkcije tega člena lahko ugotovimo, da potrebuje ta člen nekaj časa, da doseže vrednost ene enote oziroma vrednost vhodne enotine stopnice. Ti členi so torej počasni, fazni kot j med vhodno in izhodno veličino znaša vedno -90°. Negativni fazni kot pomeni, da izhodna veličina zaostaja za vhodno veličino. Zgled takega člena je enosmerni tuje vzbujani elektromotor.
- Tak člen predstavljajo vsi sestavi, pri katerih povzroči trenutna sprememba vhodne veličine ali enotina stopnica naraščanje izhodne veličine po naravni ali eksponencialni krivulji. Po določenem času se naraščanje konča in člen doseže stacionarno stanje. Dve značilni konstanti, ki opišeta člene prvega reda v smislu njihovih dinamičnih lastnosti, sta ojačenje K1 in časovna konstanta T1. Ojačenje je razmerje med velikostjo izhodne veličine in velikostjo vhodne veličine v stacionarnem stanju. Način izračunavanja časovne konstante je odvisen od vrste energije, ki se lahko hrani v členu. Časovna konstanta je čas, ki je potreben, da doseže izhodna veličina 63% svoje končne vrednosti v stacionarnem stanju. V praksi doseže izhodna spremenljivka svojo končno vrednost v času 5 (petih) časovnih konstant.
Kaj kaže slika?
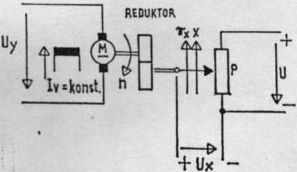
- praktičen primer proporcionalnega člena
- praktičen primer integralnega člena
- praktičen primer diferencialnega člena
- praktičen primer zakasnilnega člena
- praktičen primer PT1 člena
- praktičen primer DT1 člena ali realnega diferencialnega člena
- praktičen primer PT2 člena
Kaj kaže slika?
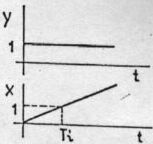
- prehodno funkcijo proporcionalnega člena
- prehodno funkcijo integralnega člena
- prehodno funkcijo diferencialnega člena
- prehodno funkcijo zakasnilnega člena
- prehodno funkcijo PT1 člena
- prehodno funkcijo DT1 člena ali realnega diferencialnega člena
- prehodno funkcijo PT2 člena
Kaj kaže slika?
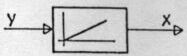
- simbol proporcionalnega člena
- simbol integralnega člena
- simbol diferencialnega člena
- simbol zakasnilnega člena
- simbol PT1 člena
- simbol DT1 člena ali realnega diferencialnega člena
- simbol PT2 člena
Kako še drugače imenujemo člen na sliki?

- delilnik napetosti
- elektromotor z reduktorjem
- tahogenerator
- transportni trak za dovajanje premoga
- diferenciator
- integrator
- vzporedni nihajni krog
Koliko elementov, ki so sposobni hraniti energijo, vsebuje vezje na sliki?


- 0
- 1
- 2
- 3
- 4
Katerega reda je torej člen, ki ga vidimo na sliki?


- člen ničelnega reda
- člen prvega reda
- člen drugega reda
- člena ni mogoče uvrstiti v nobeno od naštetih skupin
Kateri osnovni testni signal je uporabljen za določanje lastnosti člena na sliki?

- enotina stopnica
- enotin impulz
- enakomerno naraščajoča strmina z naklonom ene enote
Kako se člen na sliki odziva na vzbujanje z enotino stopnico? Kateri od opisov prehodne funkcije torej ustreza sliki?



- odziv na enotino stopnico je enakomerno naraščanje izhodnega signala in sicer za eno enoto v času integracijske konstante Ti
- odziv na enotino stopnico je prav tako enotina stopnica, le da je pomnožena z ojačevalnim faktorjem K1
- odziv na enotino stopnico je prav tako enotina stopnica, le da je zakasnjena za mrtvi čas Tm
- odziv na enotino stopnico je neskončno kratek in neskončno velik impulz, ki se pojavi istočasno s prehodom stopnice iz nizkega stanja v visoko stanje
- odziv na enotino stopnico je naravna ali eksponetna krivulja s časovno konstanto "tau", ki je po obliki enaka časovnemu poteku napetosti kondenzatorja pri polnenju
- odziv na enotino stopnico je naravna ali eksponetna krivulja s časovno konstanto "tau", ki je po obliki enaka časovnemu poteku toka skozi kondenzator pri polnenju
- odziv na enotino stopnico je krivulja, ki je enaka krivulji dušenega nihanja nihajnega kroga, pri kateri sta značilna podatka največja amplituda prenihanja Apr in perioda nihanja Tl
Kateri člen ustreza spodnjemu opisu?
Ti členi so členi, pri katerih je hitrost spremembe izhodne veličine sorazmerna velikosti vhodne veličine. Če je vrednost vhodne veličine velika, se izhodna veličina spreminja hitro, če pa je vhodna veličina majhna, se izhodna veličina spreminja počasi. Sorazmernostni faktor Ti imenujemo integracijska časovna konstanta, pove pa, v kolikšnem času se spremeni velikost izhodne veličine za eno enoto oziroma, v kolikšnem času doseže izhodni signal vrednost vhodnega signala. S pomočjo prehodne funkcije tega člena lahko ugotovimo, da potrebuje ta člen nekaj časa, da doseže vrednost ene enote oziroma vrednost vhodne enotine stopnice. Ti členi so torej počasni, fazni kot j med vhodno in izhodno veličino znaša vedno -90°. Negativni fazni kot pomeni, da izhodna veličina zaostaja za vhodno veličino. Zgled takega člena je enosmerni tuje vzbujani elektromotor.- proporcionalni člen
- integralni člen
- diferencialni člen
- zakasnilni člen
- PT1 člen
- DT1 člen ali realni diferencialni člen
- PT2 člen
Kateri opis ustreza sliki?



- Ti členi so sestavi, pri katerih je sprememba izhodne veličine sorazmerna spremembi vhodne veličine. Pri teh členih ni časovne zakasnitve med vhodnim in izhodnim signalom. To pomeni, da so ti členi neskončno hitri. Lep primer je vezje, sestavljeno iz dveh ohmskih uporov.
- Ti členi so členi, pri katerih je hitrost spremembe izhodne veličine sorazmerna velikosti vhodne veličine. Če je vrednost vhodne veličine velika, se izhodna veličina spreminja hitro, če pa je vhodna veličina majhna, se izhodna veličina spreminja počasi. Sorazmernostni faktor Ti imenujemo integracijska časovna konstanta, pove pa, v kolikšnem času se spremeni velikost izhodne veličine za eno enoto oziroma, v kolikšnem času doseže izhodni signal vrednost vhodnega signala. S pomočjo prehodne funkcije tega člena lahko ugotovimo, da potrebuje ta člen nekaj časa, da doseže vrednost ene enote oziroma vrednost vhodne enotine stopnice. Ti členi so torej počasni, fazni kot j med vhodno in izhodno veličino znaša vedno -90°. Negativni fazni kot pomeni, da izhodna veličina zaostaja za vhodno veličino. Zgled takega člena je enosmerni tuje vzbujani elektromotor.
- Pri teh členih je velikost izhodne veličine sorazmerna hitrosti spremembe vhodne veličine. Prehodna funkcija tega člena je iglasti impulz z neskončno veliko amplitudo in neskončno kratkim trajanjem. V resničnosti takega signala ni, zato imenujemo te člene idealni členi. Ko približen primer idealnega člena te vrste lahko obravnavamo tahometrični generator!
- Ti členi so dejansko tudi P-členi, le da zakasnijo izhodni signal za čas Tm ali mrtvi čas. Ti členi so skrajno nezaželeni, ker močno poslabšajo regulacijske lastnosti in povzročajo nestabilnost sistema. Take člene poskušamo iz regulacijskega kroga vedno izločiti ali pa vsaj zmanjšati mrtvi čas Tm. Primer je transport premoga iz deponije do kurišča s pomočjo tekočega traku.